Retired Techie
Getting older, not necessarily wiser!
Sierpinski Pyramid POVRay Part 1
Published on May 27, 2022 at 11:13 pm by LEWIntroduction
In this series of posts I will be walking through creating Sierpinski’s Pyramid in POV-Ray. I will be covering the math, object creation, and scene setup.
When I decided to work on this project, I looked up Sierpinski’s Pyramid on line to see if there were already existing tutorials. I found a few written for earlier versions of POVRay, that did not translate very well to POVRay 3.7 for a variety of reasons. But it is always nice not starting totally from scratch.
Boring Historical Stuff
Wacław Franciszek Sierpiński was a Polish mathematician who lived from the late 1800’s to the mid 1900’s. The Fractal set which bares his name has the shape of an equilateral triangle, and while generally made with triangles, the fractal can be generated with different base solids.
The shape is most often referred to in two dimensions as Sierpiński’s triangle or Sierpinski’s gasket. We will be using pyramid and rendering it in three dimensional space.
Basic Scene Setup
As a scene backdrop we will be using a sky sphere, and infinite plane (see this post for more information and a base file to work with). Since we will be rendering an actual object, I will be adding a second point light to improve the look of the object in the final render.
Initially I am setting the two lights at <100, 30, -100> and <-100, 30, -100>. The camera will initially be placed at <0, 5, 5>. And any object will go at <0, 0, 0>.
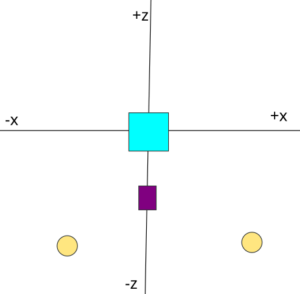
POVRay Coordinate System
The coordinate system in POVRay is somewhat different form other 3D programs. Basically looking at your screen, X is left and right, Y is up and down, and Z is depth. In the above example we are looking down along the Y access.
Building a Pyramid
A pyramid is not one of the basic shapes in POVRay, so we will need to construct one to use. Once we have created this basic shape, we will set up the programming math to duplicate, scale, and translate it to create our final render.
There are a few different ways to render a pyramid in POVRay. I am going to list three options to make a 2 x 2 x 1 pyramid, and you can chose the one that you like. I have not noticed any really large changes in rendering speed based on how the pyramid was created.
If there is any interest I will go into how each was derived, though some are self explanatory.
Isosurface Method (Red)
This was the slowest method for rendering (but not by much). I do not recommend using this method, as changing/modifying the base pyramid can be a bit problematic.
isosurface {
function {abs(x/sqrt(2))+abs(y)+abs(z/sqrt(2))-1}
contained_by {
box{ sqrt(2), <-sqrt(2),0,-sqrt(2)> }
}
max_gradient 1.4
rotate 45*y
}
Difference of Planes Method (Blue)
This method works well, but also is not the easiest to modify. It renders slightly faster than the isosurface method.
difference{
box {< 1,1,1>, <-1,0,-1>}
plane { x-y, -sqrt(2)/2 }
plane { -x-y, -sqrt(2)/2 }
plane { z-y, -sqrt(2)/2 }
plane { -z-y, -sqrt(2)/2 }
}
Mesh Method (Green)
This is my preferred method, constructing the pyramid out of a mesh of triangles. Graphing it out by hand makes it easy to visualize.
mesh {
triangle {<1, 0, 1>, <1, 0, -1>, <0, 1, 0>}
triangle {<-1, 0, 1>, <-1, 0, -1>, <0, 1, 0>}
triangle {<1, 0, -1>, <-1, 0, -1>, <0, 1, 0>}
triangle {<1, 0, 1>, <-1, 0, 1>, <0, 1, 0>}
triangle {<1,0,1>, <1,0,-1>, <-1,0,-1>}
triangle {<1,0,1>,<-1,0,-1>, <-1, 0,1>}
}
Note About Ratio
The above photo shows pyramids that are 2 x 1 x 2. The X and Z axis spans -1 to +1, and the Y axis spans 0 to +1.

In the below picture, the green pyramids now has a 1 x 1 x1 ratio.
The final rendering ratio will be directly related on the base pyramid ratio.
Conclusion
In this post we discussed some basic information related to Sierpinski’s Pyramid. We also looked at different ways to create the base pyramid structure in POVRay.
In the next post, we will discuss some basic POVRay mechanics that I will be using to make this project. After that we will discuss the math, then put everything together.
Sierpinski Pyramid POVRay Part 1
Sierpinski Pyramid POVRay Part 2


Add New Comment