Retired Techie
Getting older, not necessarily wiser!
Electronics: Ohms Law
Published on March 22, 2022 at 4:56 am by LEWIntroduction
During another post, I realized I should probably post a few articles on electrical theory. So in this first article I will cover, in brief, Ohms law.
Ohms law is named after Goerg Ohm, who in the 1820’s did research into galvanic circuits. The law states the mathematical relationship between voltage, current, and resistance. It is considered an empirical relationship that has been tested by extermination. It has been found to hold true for many application that we are likely to use it in.
Definitions
Before discussing Ohms law, we should talk about the variables used. They are not necessary intuitive
- E: This represents Electro Motive Force (or EMF). A more common term is Voltage (V). There is a difference; EMF is a force, whereas Voltage is a difference of potential. But in practicality, the difference is not relevant for our applications. We will use E here, but remember you are likely to see V used also. The unit for E is the Volt
- I: This represents intensité du courant (intensity of Current). If current was represented by C, it might be confused with capacitance. Therefore we will typically use I to represent current. While Voltage represents electrical potential, Current represents electrical flow. The unit for I is the amp.
- R: Resistance is a materials opposition to the flow (current). This is probably the most straight forward of our variables. The unit for resistance is the ohm.
Forms of Ohms law
Ohms law is usually written in one of three forms, depending on then variable being evaluated.
E = IR I = E/R R = E/I
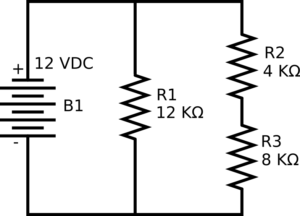
We will use the below simple test circuit to evaluate the usage of these formulas.
Analysis
The battery uses a chemical reaction to produce its Electromotive force. R1 has a potential drop across it of 12 V. It is placed across B1, a 12V DC battery. Using the second equation we can calculate the current, which is 12 V / 12000 ohms, or 0.001 Amps.
Because R2 and R3 total 12,000 ohms, the current drop across that leg is also 0.001 amps, for a total current draw of 0.002 amps.
We can calculate the voltage across R2 by using the first equation, or 0.001 Amps x 4,000 ohms = 4V. If we calculate the voltage drop across R3, we will find it is 8 V.
Importance of Relationships
Unless you are working as a technician or engineer, you are probably never going to have to actually calculate voltages and currents in a circuit. However it is important to understand the relationship between voltage, current and resistance.
In a previous post we talked about a wiring issue. From the above example we can see the relationship between current and resistance with a constant voltage. As resistance increases, current decreases. An open or broken wire has infinite resistance, so current will drop to zero. Likewise a short occurs when the hot and neutral leads touch, with a resistance of close to zero. In this case current increases until the breaker trips.
Conclusion
We took a quick look at ohms law, and as stated, the important takeaway is the relationship, not necessary the exact math. A breaker trips, or a fuse blows, you are drawing to much current, which indicates resistance has gone down someplace.
Understanding the relationship can help isolate problems more easily.

Add New Comment